Ich möcht in diesem Beitrag zeigen, dass man Signalerarbeitung auch ohne viel Theorie und Mathematik hinbekommt und hab dafür eine Bibliothek geschrieben, die klein, supereinfach zu verwenden und vorallem auf einem ESP mit Micropython ihren Dienst tuen kann.
Signalverarbeitung war eines meiner Hauptfächer im Studium und ich kann mich noch an einen kompletten Leitzordner voller Theorie und Mathematik dazu erinnern. Sucht man im Internet nach z.B. einer FFT oder einen Filter in Python so findet man Programme die Bibliotheken verwenden, die es leider für Micropython nicht gibt und für die Ausführung auf einem Mikrocontroller nicht geeignet sind.
Eigentlich ist Signalverarbeitung recht einfach. Alles fing damit an, dass ein Französischer Mathematiker Jean Baptiste Joseph Fourier schon so um 1800 rum herausgefunden hat, dass sich jedes periodische Signal aus einer Überlagerung von Sinusschwingungen zusammensetzt.
Jede Sinusschwingung wird im Spektrum des Signals als Strich dargestellt. Hat man z.B. ein andersförmiges Signal, wie z.B. ein Rechteck, so besteht das Spektrum aus mehreren Strichen unterschiedlicher Frequenz und Amplitude.
Aber zurück zu unseren Sinusschwingungen. Ich hab ein kleines Programm geschrieben, das zwei Sinusschwingungen generiert und das zugehörige Spektrum anzeigt:
#####################################################################
# Testprogramm für b2c_sft : box2code - Signal Filter Toolbox
# Stefan am 2024-01-05
#####################################################################
######## Configure here:
sampleFreq = 2000
fftLen = 512 # must be power of 2
applyNotch = True
applyWinFilterBandStop = False
########################
import matplotlib.pyplot as plt
import b2c_sft
import math
data1 = b2c_sft.generateSinus(fftLen, 100, 250, sampleFreq)
data2 = b2c_sft.generateSinus(fftLen, 50, 500, sampleFreq)
data = b2c_sft.mixSignals(data1,data2)
if applyNotch:
notch = b2c_sft.Filter(b2c_sft.notchZeroes(500,sampleFreq), b2c_sft.notchPoles(500,sampleFreq))
data = notch.filterIterative(data)
zeroes1 = [
0.98811787286546693000, # comes from WinFilter
0.00000000000000263287,
2.96435361859640080000,
0.00000000000000526575,
2.96435361859640080000,
0.00000000000000263287,
0.98811787286546693000
]
poles1 = [
1.00000000000000000000, # comes from WinFilter
0.00000000013946281840,
2.98743365009436030000,
0.00000000021746471926,
2.97494613251504750000,
0.00000000001021009398,
0.98751223597926108000
]
if applyWinFilterBandStop:
bandStopFromWinFilter = b2c_sft.Filter(zeroes1, poles1)
data = bandStopFromWinFilter.filterIterative(data)
plt.subplot(2, 1, 1)
plt.plot(data)
plt.xlabel('Sample')
plt.ylabel('Amplitude')
b2c_sft.fft(data)
plt.subplot(2, 1, 2)
plt.suptitle('Zeit- und Frequenzsignal')
plt.plot(b2c_sft.frequencyAxis(data, sampleFreq), data)
plt.xlabel('Frequenz in Hz')
plt.ylabel('Amplitude')
plt.show()
Ausschauen tut das ganze dann so (hab Thonny verwendet mit dem Lokalen Python-Interpreter. Die mathplotlib musst du dir vielleicht mit pip erst installieren – Der Code für die Bibliothek b2c_sft kommt etwas weiter unten):
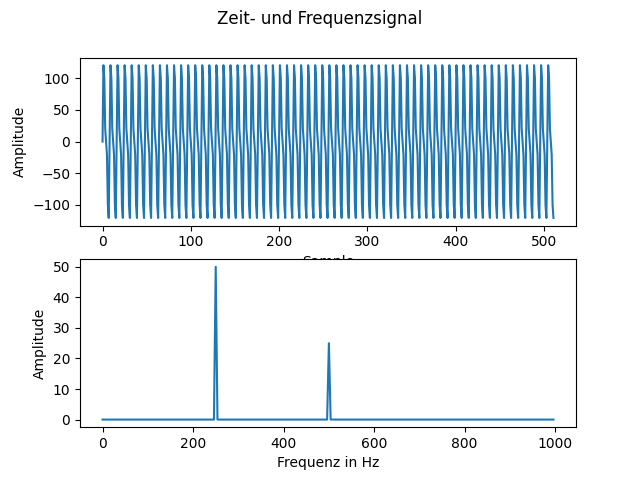
Bei Bedarf kann man zwei Filter aktivieren. Der eine ist ein NotchFilter, der gezielt eine Sinusschwingung aus dem Spektrum herausfiltert:
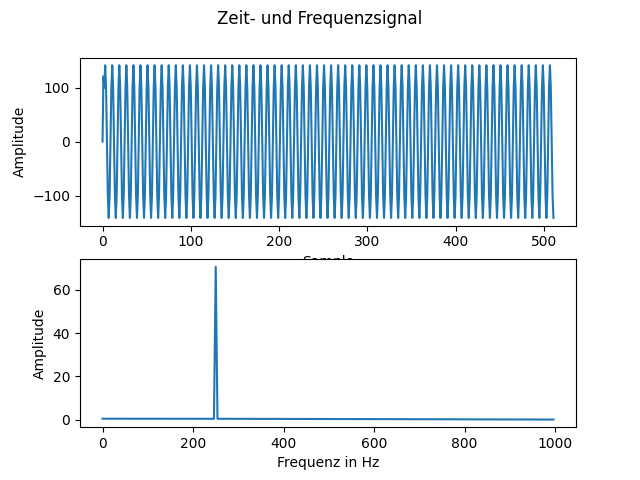
Man sieht dass die Schwingung bei 500 Hz jetzt weg ist
Du hast hier bestimmt schon ein paar Fragen:
- Die Samplefrequenz ist doch 2000 – warum geht das Spektrum nur bis 1000
Zwei andere berühmte Mathematiker haben im Nyquist-Shannon-Abtasttheorem bestimmt, dass die Abtastfrequenz mindestens doppelt so hoch sein muss wie die höchste im Signal vorkommende Frequenz. D.h. der schnellste messbare Sinus darf höchstens halb so schnell sein wie die Samplefrequenz. Tatsächlich ist eine normale FFT um den Mittelpunkt spiegelsymmetrisch und enthält auch „negative Frequenzen“ aber weil ich diese Information in der Praxis für unnötig halte halbiere ich in der Lib die FFT nach der Berechnung. Dadurch gibt es keine Verwirrung.
- Das ist doch eine Filterbibliothek – Es gibt nur einen Notch-Filter – wie mach ich andere Filter wie Tief- oder Hochpass ?
Der Filter in der Bibliothek nimmt Listen von Polen und Nullstellen als Parameter (Eigentlich die Koeffizienten eines Polynoms mit entsprechenden Nullstellen, aber ich hab ja versprochen keine Mathematik 🙂 ). Das genügt um jeden erdenklichen Filter damit zu bauen. Aber wie kommt man an die Werte für Pole und Nullstellen ?
Dazu möchte ich dir WinFilter empfehlen:
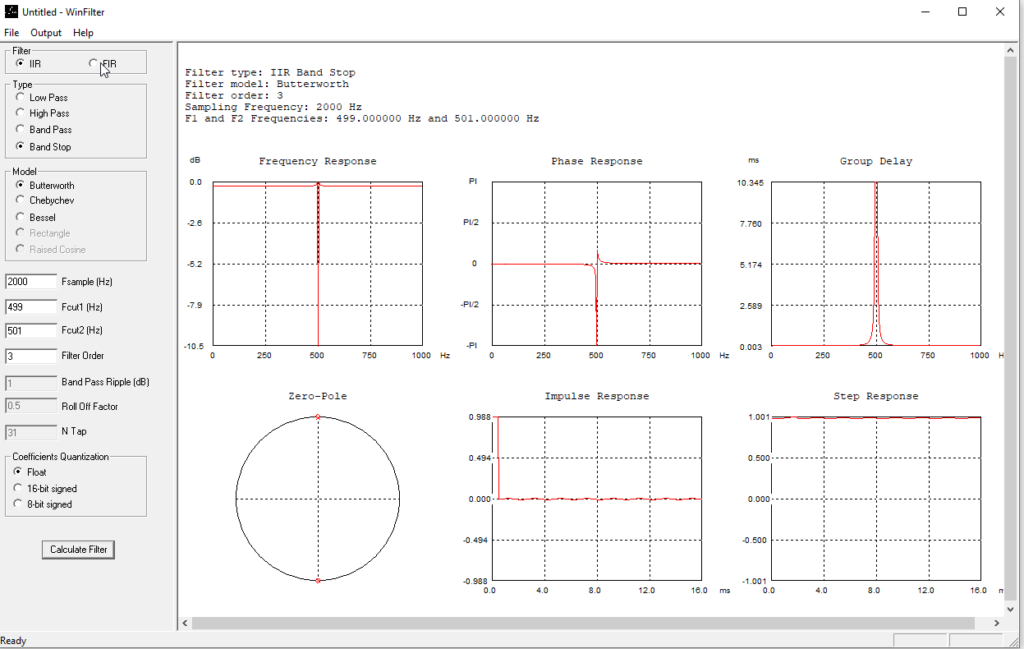
Wenn du auf „C-Code Generieren“ klickst kommt als Ergebnis folgendes:
float ACoef[NCoef+1] = {
0.98811787286546693000,
0.00000000000000263287,
2.96435361859640080000,
0.00000000000000526575,
2.96435361859640080000,
0.00000000000000263287,
0.98811787286546693000
};
float BCoef[NCoef+1] = {
1.00000000000000000000,
0.00000000013946281840,
2.98743365009436030000,
0.00000000021746471926,
2.97494613251504750000,
0.00000000001021009398,
0.98751223597926108000
};Hinweis: beim FIR-Filter gibt es nur einen Array – das sind dann deine zeroes – Übergeb dann für die pole einfach eine leere Liste.
Kopiere dir das raus und packe es, Python konform, in dein Programm. Der Rest ist einfach:
zeroes1 = [
0.98811787286546693000, # comes from WinFilter
0.00000000000000263287,
2.96435361859640080000,
0.00000000000000526575,
2.96435361859640080000,
0.00000000000000263287,
0.98811787286546693000
]
poles1 = [
1.00000000000000000000, # comes from WinFilter
0.00000000013946281840,
2.98743365009436030000,
0.00000000021746471926,
2.97494613251504750000,
0.00000000001021009398,
0.98751223597926108000
]
bandStopFromWinFilter = b2c_sft.Filter(zeroes1, poles1)
data = bandStopFromWinFilter.filterIterative(data)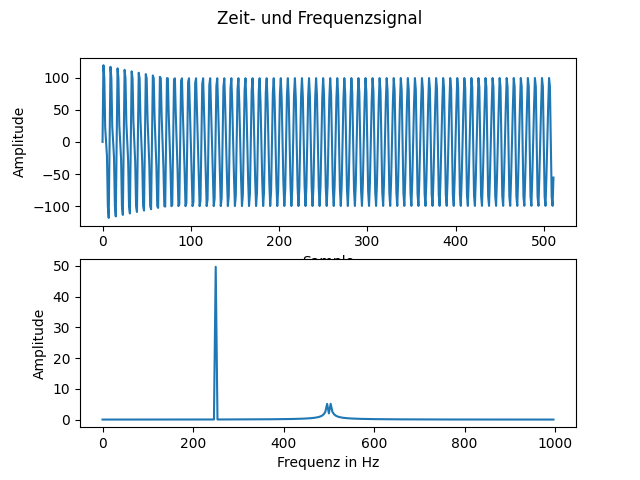
Du siehst, dass du den Sinus bei 500 Hz auch mit einer Bandsperre aus WinFilter ausblenden kannst (leider nicht so exakt wie mit dem Notch. Der Notch ist Teil der Bibliothek, weil WinFilter diesen nicht anbietet, ich ihn aber für sehr sehr nützlich halte)
Mit diesen paar kleinen Hilfsmitteln kannst du schon die meisten Filteraufgaben lösen.
Und auf den ESP damit 🙂
Hier einfach ein Cheap-Yellow-Display als Referenzplatform
Benchmark
Als erstes brauchen wir ein Gefühl dafür wie lange die Berechnung einer FFT dauert. Dazu ein kleines Testprogramm:
import b2c_sft
import utime
lens = [16, 32, 64, 128, 256, 512, 1024, 2048]
for fftLen in lens:
data = b2c_sft.generateSinus(fftLen, 100, 250, 2000)
start = utime.ticks_us()
b2c_sft.fft(data)
time = utime.ticks_us() - start
print("FFT-Länge " + str(fftLen) + " => " + str(time) + " us = " + str(time / 1000) + " ms")
""" Ausgabe:
FFT-Länge 16 => 3476 us = 3.476 ms
FFT-Länge 32 => 5576 us = 5.576 ms
FFT-Länge 64 => 10649 us = 10.649 ms
FFT-Länge 128 => 21342 us = 21.342 ms
FFT-Länge 256 => 48962 us = 48.962 ms
FFT-Länge 512 => 97913 us = 97.91301 ms
FFT-Länge 1024 => 219556 us = 219.556 ms
FFT-Länge 2048 => 494714 us = 494.714 ms
"""Sehr schön zu sehen ist, dass wir bei jeder Verdoppelung der FFT-Größe etwa doppelt so lange brauchen. Eine 512er FFT in ca. 100 ms find ich schon ganz anständig – damit kann man was anfangen 🙂
ESP-Programm
Das erste ESP-Programm hat nur etwa 50 Zeilen und zeigt die FFT mit dem lvgl-Chart an. Ist eine 512er FFT mit 2kHz Abtastrate. Man sieht, dass das schon ziemlich flüssig geht.
Das Eingangssignal ist ein (von meinem Taschenoszi mit Funktionsgenerator) generierter 500 Hz Sinus mit 1V Amplitude – Eingespeist am ADC von GPIO35 des ESPs. Dieser liegt, wie erwartet, genau in der Mitte des Spektrums (0 bis 1000 Hz)
#####################################################################
# Testprogramm für b2c_sft : box2code - Signal Filter Toolbox
# Stefan am 2024-01-05
#####################################################################
import machine, time
import uasyncio
import b2c_sft
import lvgl as lv
import display_driver
adc = machine.ADC(machine.Pin(35))
adc.atten(machine.ADC.ATTN_11DB)
adc.width(machine.ADC.WIDTH_9BIT)
tim = machine.Timer(1)
tsf = uasyncio.ThreadSafeFlag()
SAMPLE_FREQ = 2000
FFT_LEN = 512
data = []
timerStop = False
def newAdcVal(p):
global timerStop, tsf
if timerStop:
return
data.append(adc.read() - 256)
if len(data) == FFT_LEN:
timerStop = True
tsf.set()
chart = lv.chart(lv.scr_act())
chart.set_size(300, 220)
chart.align(lv.ALIGN.CENTER, 0, 0)
chart.set_range(lv.chart.AXIS.PRIMARY_Y, 0, 5000)
chart.set_style_size(0, lv.PART.INDICATOR)
ser = chart.add_series(lv.palette_main(lv.PALETTE.RED), lv.chart.AXIS.PRIMARY_Y)
chartData = []
for i in range(0, FFT_LEN // 2):
chartData.append(0)
pcnt = len(chartData)
chart.set_point_count(pcnt)
chart.set_ext_y_array(ser, chartData)
def run():
global timerStop
while True:
await tsf.wait()
b2c_sft.fft(data)
for i in range(0, len(data)):
chartData[i] = int(100 * data[len(data) - i - 1])
chart.set_ext_y_array(ser, chartData)
chart.refresh()
data.clear()
print("DONE")
timerStop = False
tim.init(freq=SAMPLE_FREQ, mode=machine.Timer.PERIODIC, callback=newAdcVal)
uasyncio.run(run())So wie filtert man denn dann jetzt ?
Dazu gehört jetzt nicht mehr viel. Definiere dir im ESP-Programm deinen Wunschfilter (hier wieder ein Notch) – Die Werte vom ADC müssen jetzt nur noch durch den Filter „durch“ – geschafft 🙂
notch = b2c_sft.Filter(b2c_sft.notchZeroes(500,SAMPLE_FREQ), b2c_sft.notchPoles(500,SAMPLE_FREQ))
def newAdcVal(p):
global timerStop, tsf
if timerStop:
return
data.append(notch.filterReal(adc.read() - 256))
if len(data) == FFT_LEN:
timerStop = True
tsf.set()Zum Ausprobieren einen Sinus von 0 bis 1000 Hz wobbeln – bei ca. 500 Hz sollte die Spitze verschwinden
Bibliothek
Die Bibliothek enthält natürlich wieder Bestandteile aus anderen Projekten:
- Hauptteil der FFT aus SimpleFFT – eine schöne kleine C++ Bibliothek, die ich schon in ein paar C++ Projekten benutzt habe
- Notch-Berechnung von hier
- Filter aus generiertem Code von WinFilter abgeleitet
#####################################################################
# b2c_sft : box2code.de - Signal Filter Toolbox
# Stefan am 2024-01-05
#####################################################################
import math
def isPowerOfTwo(num):
return num and (not(num & (num - 1)))
def rearrangeData(data):
num_elements = len(data)
buf = complex(0,0)
target_index = 0
bit_mask = 0
for i in range(0, num_elements):
if target_index > i:
buf = data[target_index]
data[target_index] = data[i]
data[i]= buf
bit_mask = num_elements
while True:
bit_mask = bit_mask >> 1
if not (target_index & bit_mask):
break
target_index &= ~bit_mask
target_index |= bit_mask
def makeTransform(data):
counter = 0
num_elements = len(data)
local_pi = -math.pi
nextbit = 0
match = 0
sine = 0.0
delta = 0.0
mult = complex(0,0)
factor = complex(0,0)
product = complex(0,0)
i = 1
while i < num_elements:
nextbit = i << 1
delta = local_pi / i
sine = math.sin(0.5 * delta)
mult = complex(-2.0 * sine * sine, math.sin(delta))
factor = complex(1.0)
for j in range(0,i):
k = j
while k < num_elements:
counter += 1
match = k + i
product = data[match] * factor
data[match] = data[k] - product
data[k] += product
k += nextbit
factor = mult * factor + factor;
i = i << 1
return True
def backToReal(data):
num_elements = len(data)
for i in range(0, num_elements):
data[i] = abs(data[i]) / num_elements
def fft(data):
if not isPowerOfTwo(len(data)):
print ("Not power of 2 !!!")
return False
rearrangeData(data)
if not makeTransform(data):
return False
backToReal(data)
n = len(data)
for i in range(0, n // 2):
data.pop()
return True
def frequencyAxis(data, fs):
num_elements = len(data)
axis = []
for i in range(0, num_elements):
axis.append(fs / num_elements / 2 * i)
return axis
def generateSinus(num_elements, amplitude, f, fs):
sinus = []
ta = 1 / fs
t = 1/f
for i in range(0, num_elements):
sinus.append(amplitude * math.sin(i * 2*math.pi*ta/t))
return sinus
def mixSignals(sig1, sig2):
num_elements = min(len(sig1),len(sig2))
data = []
for i in range(0, num_elements):
data.append(sig1[i] + sig2[i])
return data
def notchPoles(f, fs):
poles = []
return poles
def notchZeroes(f, fs):
zeroes = [0,0,0]
zeroes[0] = 1.0
zeroes[1] = -2.0 * math.cos(2 * math.pi * f / fs)
zeroes[2] = 1.0
return zeroes
def iirNotchZeroes(f, fs):
b0=1.0
b1=-2.0*math.cos(2.0*math.pi*f/fs);
b2=1.0;
return [b0,b1,b2]
def iirNotchPoles(f, fs):
r=0.9;
a0=1.0
a1=-2.0*r*math.cos(2.0*math.pi*f/fs)
a2=r*r
return [a0,a1,a2]
class Filter:
def __init__( self, zeroes, poles ):
self.zeroes = zeroes
self.poles = poles
self.filterlen = len(zeroes)
self.x = []
self.y = []
for i in range(0, self.filterlen + 1):
self.y.append(0.0)
self.x.append(0.0)
def filterReal(self, newSample):
# shift old samples
for i in range(self.filterlen, 0, -1):
self.x[i] = self.x[i-1]
self.y[i] = self.y[i-1]
# calc new output
self.x[0] = newSample
self.y[0] = self.zeroes[0] * self.x[0];
for n in range(1, self.filterlen):
self.y[0] += self.zeroes[n] * self.x[n]
if len(self.poles) > 0:
self.y[0] -= self.poles[n] * self.y[n]
return self.y[0]
def filterIterative(self, data):
output = []
for newSample in data:
output.append(self.filterReal(newSample))
return output
def hammingWindow(data):
for n in range(0, len(data)):
data[n] = data[n] * (0.54 - 0.46 * math.cos((2 * math.pi / len(data)) * n))